The intention behind GEVfoil is to establish an open-source set of Python classes to handle aerofoils (American English: airfoils). The intention is that these can be used for anything from generating simple point clouds, analytical representations all the way to STL files for CFD meshing and OpenFOAM BlockMesh output.
The first step is starting with something basic, in this case a simple class to generate NACA 4 series aerofoils:
import numpy as np
import matplotlib.pyplot as plt
class NACA4(object):
"""A class for generating NACA 4 series aerofoils
TO-DO - linspace not good at LE capture """
def __init__(self, foil, points=200, chord=1):
super(NACA4, self).__init__()
m = float(foil[0])/100 # max camber
p = float(foil[1])/10 # chordwise position of max camber
t = float(foil[2:])/100 # thickness
x = np.linspace(0, chord, points)
self.x = x
yt = self.thickness(x, t)
yc = []
for coord in x:
if m:
yc.append(self.camber(m, p, coord))
else:
# No camber
yc.append(0)
y1 = yc + yt
y2 = yc - yt
self.y = y1
plt.plot(self.x, yc)
plt.plot(self.x, y1, '.')
plt.plot(self.x, y2, '.')
plt.axis('equal')
plt.show()
def thickness(self, x, t):
# Y thickness at given x point
return t / 0.2 * \
(0.2969*np.sqrt(x)-0.126*x-0.3516*x**2+0.2843*x**3-0.1015*x**4)
def camber(self, m, p, x):
# Return the camber of the aerofoil
if x <= p:
return m/p**2 * (2*p*x-x**2)
return m/(1-p)**2*((1-2*p)+2*p*x-x**2)
if __name__ == "__main__":
test = NACA4('2412')
For now, Matplotlib has been built into the class for visual reference. For example, 2412 generates:
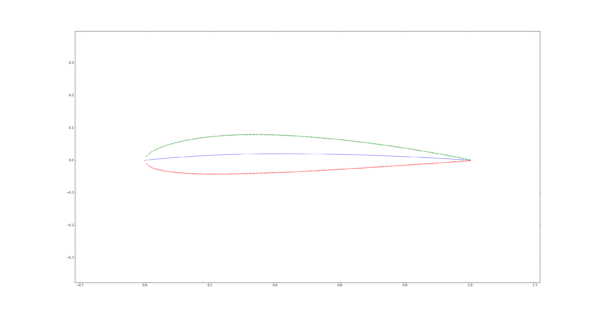
And 0010 creates:
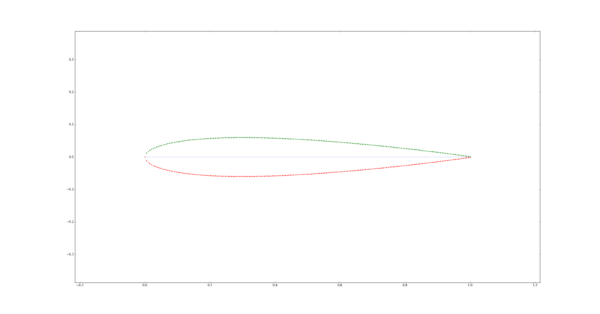
At this stage there is a clear issue around the leading edge, the function was interrogated with a linearly spaced x/chord-wise interval, this must be improved for the future to cluster points around the greatest curvature.
